Влияние маневрирования лесных машин на уплотнение почвогрунтов лесосеки

Сохранение плодородия лесных почв и улучшение их лесорастительных свойств является одним из магистральных направлений научно-технического прогресса в лесозаготовительном производстве. Негативное влияние на лесные почвогрунты при разработке лесосек оказывают лесосечные машины и персонал. Под воздействием движителей лесосечных машин и древесины почва уплотняется, разрушается ее структура и, как следствие, снижается плодородие.

В результате ливневых дождей из колей, оставленных колесами и гусеницами лесных машин, могут вымываться с одного гектара сотни кубометров плодородного слоя почвы. Считается, что восстановление почвенного покрова и плодородия почвы лесосеки произойдет через несколько десятилетий, что резко снижает как экологический эффект, так и продуктивность лесов.

На развитие оставляемых на доращивание деревьев и на всю экосистему в целом значительное влияние оказывают машины и технологические процессы лесосечных работ. В числе основных факторов этого влияния можно отметить повреждения стволов оставляемых на корню деревьев, а также минерализацию и переуплотнение лесных почвогрунтов.

Повсеместное применение сплошных концентрированных рубок за 70 лет их проведения привело к существенному изменению структуры всего лесного фонда. В результате этих рубок на месте коренных еловых, сосновых и лиственничных лесов формируются новые, менее производительные, преимущественно лиственные леса с участием хвойных пород. Значительно сократились площади спелых сосновых лесов, а лиственница становится реликтовой породой.

Наиболее интенсивное отрицательное воздействие на почвогрунты при разработке лесосек оказывают трелевочные системы (трактор с пачкой древесины). Доказано, что воздействие тракторной трелевки на поверхность вырубок может как ухудшать, так и улучшать ее лесорастительные свойства.

При исследовании процессов деформации и уплотнения почвогрунта под воздействием движителей лесных машин и трелевочных систем (ТС) широкое распространение получили такие одномерные модели, рассматривающие процесс воздействия движителя на почвогрунт, как вдавливание в него штампа.

Цель исследования объемной модели деформирования грунта в главных напряжениях - минимизация вредного воздействия техники на подрост и его корневую систему при многократном проходе ТС, что обусловлено требованием движения по заранее намеченным трассам волоков.

Однако при трелевке точно выдержать заданное направление движения не представляется возможным, и трактор вынужден неоднократно совершать поворотные движения. В этом случае грунт находится в объемном напряженно-деформированном состоянии и напряжения возникают на произвольных, в общем случае не главных площадках, что обусловливает возникновение дополнительных касательных напряжений в направлении, перпендикулярном действию нормальной нагрузки.

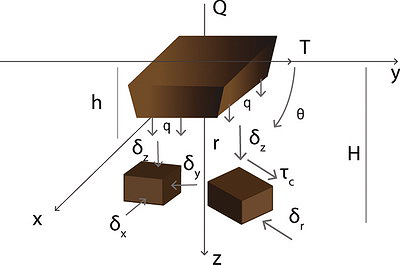
Рис. 1. Схема объемного напряженного состояния грунта при повороте штампа

Рассмотрим (рис. 1) действие на грунт сосредоточенной силы Q = G + Q₁, где: G - сила тяжести трактора, Q₁ - сила тяжести пачки, погруженной на трактор. Процесс деформирования грунта происходит в пространственной декартовой системе координат xyz, оси которой принимаются главными, а на элементарных площадках массива действуют соответствующие этим координатам главные напряжения σ₁ = σ_z, σ₂ = σ_y и σ₃ = σ_x, тогда как касательные напряжения отсутствуют.

В процессе погружения движителя (штампа) на глубину h происходит уплотнение грунта, который испытывает действие вертикальной нагрузки (вертикального давления) q. Поскольку к штампу кроме вертикальной силы Q приложена касательная (горизонтальная) сила Т тяги трактора, возникает деформация грунта в направлении действия этой силы, следствием чего является формирование горизонтальной нагрузки τ_с (горизонтального давления), характеризующей величину удельного сопротивления грунта срезу.

В момент маневра трактора и отклонения ТС от заданного направления движения на угол θ деформирование грунта целесообразно рассмотреть в цилиндрической системе координат zrθ. Компоненты тензора напряжений в этой системе в общем случае при наличии касательных напряжений τ_rθ, совпадающих по направлению с действием нагрузки τ_с, определяются соотношениями:

На рис. 4 для трех значений углового параметра θ: 5, 10 и 15° - при значении r = 0,05 м (в непосредственной

т. е. кривыми, равноудаленными друг от друга, что свидетельствует о качественной однородности процесса увеличения нагрузки на грунт при разных значениях угла поворота трелевочного трактора, однако представленные на графиках количественные отличия приведенного давления от величины погружения грунтозацепа обусловлены дополнительными касательными напряжениями.

трелевочный трактор проходит N раз по одному и тому же участку трассы, оценивается с помощью формулы

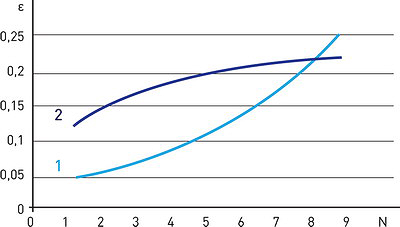
Рис. 5. Изменение деформаций с ростом числа циклов проходки:
1 – упругая деформация, ε₁ (у = 0,0433Ln(x) + 0,1195 R² = 0,9846);
2 – вязкопластическая деформация, ε₂ (у = 0,0386е^0,2061х R² = 0,9161)

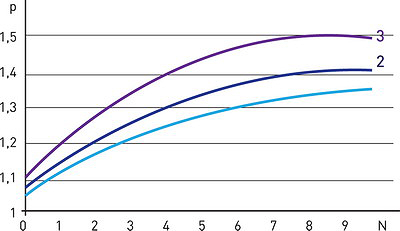
Рис. 4. Зависимости приведенного давления от величины погружения грунтозацепа:
1 – θ = 5^o (у = 28,594ln(x) + 200,94 R² = 0,9417);
2 – θ = 10^o (у = 31,702ln(x) + 176,48 R² = 0,9381);
3 – θ = 15^o (у = 36,864ln(x) + 157,48 R² = 0,9464)

Вязкопластическая деформация грунта ε₂ характеризует вторую фазу процесса уплотнения, когда сила сопротивления уплотнению соизмерима с силой сопротивления сдвигу.

На рис. 5 представлены в графическом виде зависимости ε₁(N) - кривая 1 и ε₂(N) - кривая 2, анализ которых показывает, что по достижении определенного числа циклов (для приведенного примера расчета N ≥ 6) вязкопластическая деформация ε₂ почти не растет, тогда как упругая деформация ε₁ продолжает расти. В механике грунтов этому состоянию соответствует этап завершения процесса переупаковки грунта, а дальнейшее уплотнение возможно только с развитием упругих деформаций.

Абсцисса точки пересечения кривых 1 и 2 на рис. 5 соответствует значению N = 8 и состоянию равенства ε₁= ε₂. Это значит, что при восьмикратном проходе ТС по одному и тому же волоку процесс уплотнения достиг предельного значения.

углового параметра θ = 0, 10 и 25° (кривые 1, 2 и 3 соответственно) представлено в графическом виде на рис. 6.

По достижении параметра N значений N ≥ 7 графики выходят на свои асимптоты, т. е. дальнейшего уплотнения почти не происходит, и можно полагать, что произошли необратимые структурные изменения элементов массива грунта и процесс его упаковки завершен.

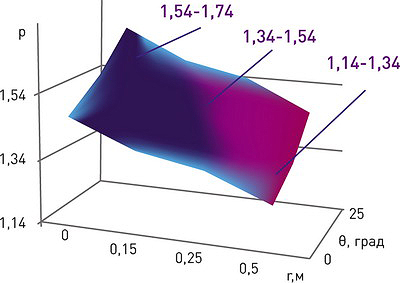
Рис. 7. Зависимость относительного уплотнения грунта от угла поворота ТС и удаления от границ волока 

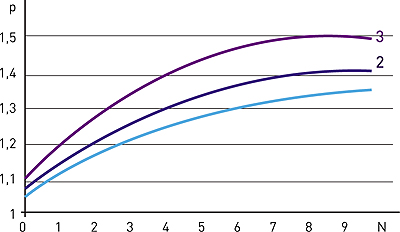
Рис. 6. Зависимости (N) с учетом изменения угла поворота ТС:
1 – θ = 0 (у = -0,0081х² + 0,1237х+1,0722 R² = 0,9462);
2 – θ = 10 (у = -0,0056х² + 0,0919х + 1,0462 R² = 0,9645);
3 – θ = 25 (у = -0,0041х² + 0,0752х + 1,0252 R² = 0,9867)

исследования процесса уплотнения грунта в зависимости от изменения исходных параметров с целью его стабилизации в зонах, непосредственно прилегающих к границам волока.

Реализация разработанной математической модели в широком диапазоне изменений параметров h, r, N и θ, графическое отражение полученных результатов в виде аппроксимирующих линий трендов и адекватный подбор уравнений с величиной детерминации не ниже R² = 0,93 позволили получить следующую многопараметрическую функцию для оценки величины относительного уплотнения грунта:

Эти зависимости можно использовать в качестве номограмм для определения предельных размеров охранных зон r_d, соответствие которым позволяет минимизировать вредное воздействие ТС на корневую систему подроста.

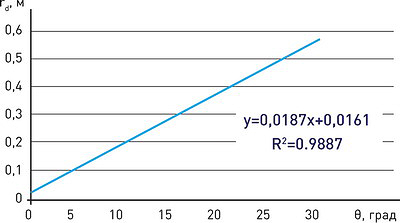
Рис. 9. Зависимость размеров зоны rd от величины угла θ

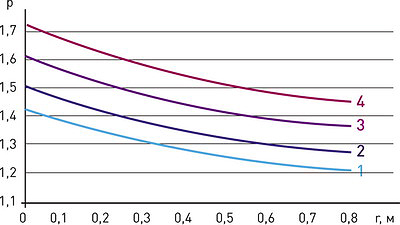
Рис. 8. Изменение уплотнения почвы по мере удаления от границы волока: 1 – N = 1; 2 – N = 3; 3 – N = 6; 4 – N = 9

Так, задавшись величиной допустимого уплотнения почвы = 1,6 при максимальном числе проходов ТС, равном N = 9, и поворотах трактора на угол, не превышающий 15°, можно выяснить, что величина rd ≈ 0,3 м.

В общем случае величину r_d можно выразить из (7) в виде

зависимость r_d от угла θ.

Аналогичные исследования были проведены при погружении движителя на глубину h = 1,5·l_d = 0,195 м и h = 2l_d = 0,26 м, т. е. моделировались условия глубокого погружения в колею волока.

На рис. 10 представлены графики, иллюстрирующие результаты расчетов, где линии 1, 2 и 3 соответствуют трем значениям относительной величины погружения грунтозацепа.

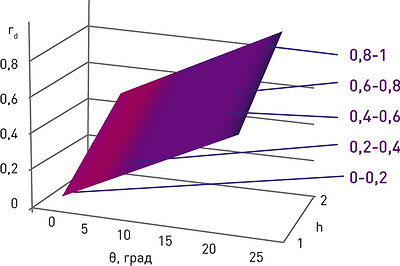
  Рис. 11. График функции rd(θ,) 

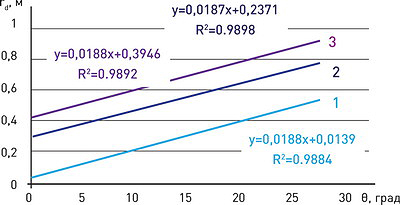
Рис. 10. Зависимость размеров зоны rd от величины угла θ с учетом глубины погружения грунтозацепа:

Как видно из данных графиков, угловые коэффициенты всех трех прямых почти совпадают, тогда как свободный

  r_d(θ, )=0,019·θ+0,38(h-1)+0,04.   (9)

глубокое погружение движителя, характерное для трелевки по податливым и мягким грунтам на большей части лесопокрытой площади России в теплый период года, в сочетании с ростом углов поворота трелевочного трактора обуславливают увеличение деформации почвогрунта в боковых полосах трелевочного волока и необходимость соответствующего этой деформации существенного увеличения размеров охранных зон.

Если первый фактор - состояние грунта - задается внешними условиями и не поддается корректировке, то второй фактор - угловой - в значительной мере зависит от квалификации оператора, подготовки волока, грамотно выбранной схемы расположения трелевочных волоков и технологии разработки лесосеки.

Однако очевидно, что точно выдержать направление движения трактора не представляется возможным, и наиболее

и r_d.

В этой связи авторами в 2012 году была поставлена и решена следующая задача стохастического моделирования (с помощью метода Монте-Карло) зависимости величины r_d от отклонения углового параметра θ.

С помощью программы выработки случайных чисел ζ_i, i = 1...n, нормально распределенных в интервале (-1, 1) с нулевым математическим ожиданием и единичной дисперсией, определялось n значений угла θ:

θ_i = M₀(θ)+ ζ_i · σ₀(θ) , i = 1,2...n, (10)

где M₀(θ) и σ₀(θ) - математическое ожидание и среднее квадратичное отклонение (СКО) угла θ.

Коэффициент вариации v(θ) = σ₀(θ)/M₀(θ) принимается в качестве обобщенной характеристики изменчивости углового параметра.

Полученные значения углов θ_i использовались в (8) для определения выборки из n значений размеров зоны r_d  и ее математического ожидания М(r_d).

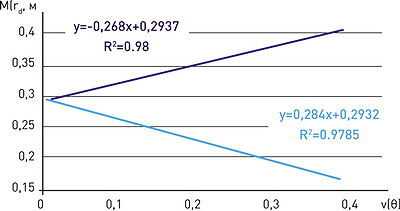
Рис. 12. Границы диапазона М(rd) в зависимости от v(θ):
1 – минимальные допустимые границы диапазона изменения величины М(rd) от коэффициента вариации v(θ); 2 – максимальные допустимые границы диапазона изменения величины М(rd) от коэффициента вариации v(θ)

На рис. 12 при следующих исходных данных: h = 0,13; N ≥ 7 и = 1,6 представлены зависимости, определяющие минимальные и максимальные допустимые границы диапазона изменения величины М(r_d) от коэффициента вариации v(θ).

Как следует из данных на рис. 12, область допустимых значений величины М(r_d) расширяется с ростом величины v(θ), т. е. в условиях изменчивости границ волока и необходимости маневров трактора проблема стабилизации параметров процесса уплотнения почвы в зоне корневой системы подроста является значимой.

В инженерных расчетах статистически значимые выборки соответствуют значениям v(θ) ≤ 0,3. Для данного примера расчета, как следует из данных, приведенных на рис. 12, допустимый диапазон изменения величины М(r_d) - от 0,22 до 0,37 м и в среднем составляет 0,3 м.

Полученные на первом этапе стохастического моделирования результаты основывались на предположении, что величина СКО σ₀(θ) является только функцией одного аргумента - угла θ.

Однако, рассматривая процесс циклического уплотнения почвы, необходимо принять во внимание, что по мере увеличения циклов прохода ТС по одному и тому же волоку происходит углубление колеи и, как следствие, снижение абсолютных значений СКО угла θ.

Полагая, что указанная величина СКО является в общем случае функцией двух переменных (θ и N), обоснуем вид функции СКО σ(θ, N).

Известна экспоненциальная связь между приростом глубины колеи Δh и параметра N:

Δh = exp(k₁ + k₂N),  (11)

где k₁и k₂ - экспериментальные коэффициенты.

Выполненные в рамках разработанной модели исследования по изменению относительной деформации Δε с ростом числа N позволили с достаточной степенью точности (не менее R² = 0,8664) получить следующее соотношение:

Δε = µ·exp(-λ·N),             (12)

где коэффициенты µ и λ зависят от величины нагрузки Q, параметров штампа и физико-механических свойств грунта.

Для примера расчета при исходных данных: h = 0,13; N ≥ 7 и = 1,6 воспользуемся зависимостью (12):

Δε = 0,1106 exp(-0,2241N).             (13)

Допуская, что с ростом N снижение СКО углового параметра напрямую определяется снижением относительной деформации при уплотнении почвы в границах колеи, предложим следующую зависимость для оценки функции σ(θ, N):

σ(θ, N) = σ₀(θ) exp(-0,2241N).          (14)

Используя соотношение (14) в сочетании со схемой (10) по выработке угловых значений θ_i при последующих расчетах относительного уплотнения с помощью (7), можно получить выборки соответствующих углу поворота трактора значений величины , i = 1, ... n.

В итоге, после обработки полученных выборок устанавливаются: математическое ожидание М() и СКО σ(), позволяющие определить границы допустимого диапазона изменения величины :

_max = М()+σ(), _min = М()-σ().   (15)

На рис. 13 для двух значений параметра удаленности от границ волока представлены графики зависимостей: 1 - _min (N) и 2 - _max (N) при h = 0,13 м, M0(θ) = 10 и σ0(θ) = 5°.

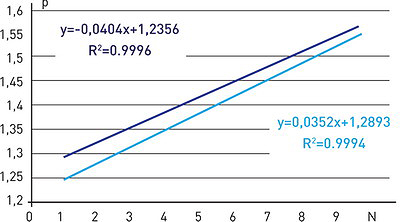
б) r = 0,05 м

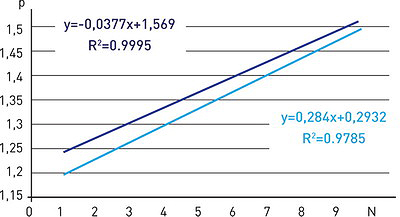
а) r = 0,25 м

Рис. 13. Диапазон изменения с ростом N: 1 – _min (N); 2 – _max (N)

Анализ полученных результатов свидетельствует о том, что по мере роста параметра N диапазон изменения величины сужается, что обусловлено механическими деформациями грунта и развитием процесса его упаковки. Иными словами, относительные значения СКО имеют тенденцию к снижению с ростом параметра N.

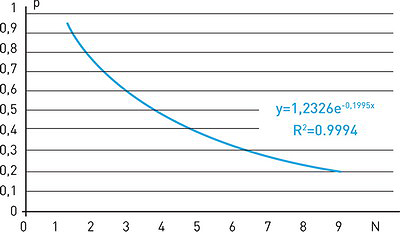
Этот вывод иллюстрируют данные, представленные на рис. 14, где наблюдается (рис. 14 а) весьма существенное относительное снижение величины СКО () с ростом величины N.

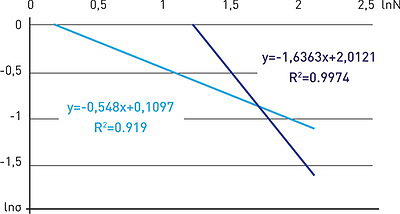
б)

а)

Рис. 14. Влияние параметра N на величину СКО : 1 – стадия интенсивного развития процесса уплотнения; 2 – затухание процесса уплотнения

Как следует из данных, представленных на рис. 14 б, в результате линеаризации кривой () с помощью логарифмических координат есть возможность установить точку пересечения прямых, которая отражает в исходных координатах точку сопряжения ниспадающей и асимптотической ветвей кривой ().

Первая ветвь характеризует стадию интенсивного развития процесса уплотнения, а вторая - его затухание и приближение к определенному предельному значению.

В результате выполненных расчетов установлено, что в условиях поставленной задачи основной процесс уплотнения почвы реализуется после достижения 6-7 циклов прохода ТС, что удовлетворительно корреспондируется с данными рис. 6.

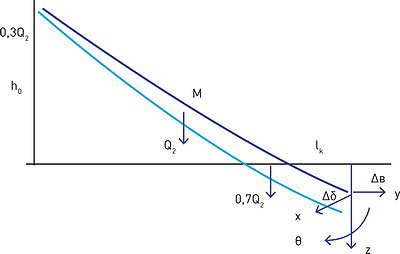
Рис. 15. Расчетная схема воздействия трелюемой пачки на почвогрунт при погружении комлевой части хлыста в почву: Q2 – вес хлыста, приложенный к центу масс М пачки; hо и lк –высота подъема пачки и длина касания почвы комлевой частью соответственно; Δв и Δδ – глубина погружения комлевой части в момент поворота в вертикальном и боковом направлениях соответственно

Таким образом, результаты математического моделирования свидетельствуют о том, что величина углового параметра θ оказывает существенное влияние на процесс циклического уплотнения грунта. Этот параметр необходимо учитывать в прогнозных оценках размеров зон охранных полос, снижающих вредное воздействие ТС на корневую систему подроста, а также деревьев, оставляемых на доращивание при выборочных рубках. При этом трелевка по мягким и податливым грунтам требует корректировки указанных размеров охранных зон в соответствии с установленными линейными зависимостями.

Вариации углового параметра θ вызывают дополнительные деформации сдвига грунта, что негативно сказывается на развитии процесса его уплотнения. Это обуславливает необходимость соблюдения таких параметров трелевки в пределах заданных границ волока, при которых с учетом установленных размеров охранных полос обеспечивается стабилизация процесса уплотнения грунта в заданных диапазонах в зоне корневой системы подроста.

Наряду с выполнением оценки воздействия движителя трелевочного трактора на процесс уплотнения грунта рассмотрим этот процесс с учетом особенностей воздействия трелюемой пачки хлыстов или деревьев на почву при возможном повороте трелевочной системы и возникающих давлений на боковую поверхность волока.

На рис. 15 представлена расчетная схема воздействия трелюемой пачки на почвогрунт при погружении комлевой части хлыста в почву, дополненная с учетом возможного поворота трелевочной системы на угол θ.

Величина погружения Δδ в рамках принятой расчетной модели с учетом коэффициента бокового распора к_б = ν/(1-ν) может быть определена по формуле

хлыста; r_t - условный радиус комля, определяемый на основании таксационных зависимостей как r_t = 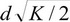, где K - коэффициент, учитывающий форму ствола (для сосны - 0,45; ели - 0,50; березы - 0,40; осины - 0,41).

Расчет величины Δδ по формуле (16) произведен при трелевке хлыстов сосны и следующих значениях входящих параметров: Q₂ = 20 кН; А = 0,1 м. е.; n = 0,7; ν = 0,35; d = 0,18 м; r_t = 0,19 м; β = 1; L = 8 м; h_o = 1,7 м.

В результате расчетов получено значение Δδ = 0,125 м.

Тогда максимальную плотность ρ_max почвы в пределах боковой поверхности волока определим как:

ρ_max= ρ_о(1+ Δδ/Н),             (17)

где Н - глубина зоны распространения деформаций, м.

При Н = 0,38 м (грунты низкой несущей способности) величина ρ_max составила 1,33 ρ_о, т. е. величина относительно уплотнения = 1,33 боковой поверхности волока достигает величины, значение которой соизмеримо со значением вертикального уплотнения после второго цикла прохода трелевочной системы при угле ее поворота на θ = 0,25° (рис. 6).

На рис. 16 представлена зависимость от Q₂ при постоянстве остальных исходных данных, которая с высокой степенью точности подчиняется логарифмическому закону.

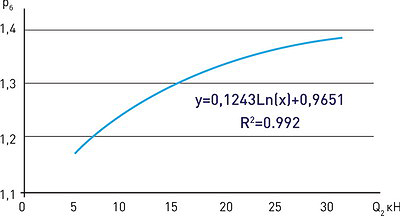
Рис. 16. Влияние веса хлыста на величину относительного уплотнения почвы в боковой части волока

Выполненные расчеты свидетельствуют о том, что наряду с оценкой величины уплотнения грунта в вертикальном направлении необходимо при поворотах трелевочной системы учитывать развитие процесса уплотнения в перпендикулярном направлении, т. е. в пределах боковой поверхности волока.

Для проверки адекватности изложенных выше теоретических положений авторами были проведены в 2012 году экспериментальные лабораторные исследования, в ходе которых использовался почвогрунт, отобранный с опытного участка Лисинского учебно-опытного лесхоза. Исходная плотность грунта составляла ρ₀ = 750-850 кг/м³, которую принимали в качестве начальной плотности почвы, или плотности естественного сложения среды.

В наших исследованиях основными задачами, решаемыми при помощи лабораторных экспериментальных исследований, являлись: получение сведений об адекватности разработанной математической модели оценки процессов деформирования при циклическом уплотнении почвогрунта и уплотнении почвогрунта в боковых полосах трелевочного волока с учетом маневрирования трактора, получении закономерности пространственного формирования касательных напряжений в боковых полосах трелевочного волока в зависимости от угла поворота трелевочной системы, а также закона распределения во времени касательных напряжений в боковых полосах трелевочного волока в зависимости от угла поворота трелевочной системы.

Для формирования образцов и придания грунту разной плотности использовался прибор стандартного уплотнения, с помощью которого создавались опытные образцы трех категорий плотности: I - ρ = 1,35-1,45, II - ρ = 1,45-1,55 и III - ρ = 1,55-1,65 т/м³.

Опытным путем были определены влажность на границе текучести W_Т = 44% и влажность на границе раскатывания W_р = 32%. В результате было установлено число пластичности для этого почвогрунта W_пл= 12, и в дальнейшем он был классифицирован по влажности с выделением трех категорий: сухой, влажный и переувлажненный.

На первом этапе осуществлялась проверка обобщенного закона Кулона, описываемого линейным уравнением (5).

Сопротивление грунта сдвигу (срезу) и соответствующая сдвигу величина τ_с  определялись по нормативам ГОСТ 12248-78 на сдвиговом приборе в зависимости от величины вертикальной нагрузки q. Для каждой серии экспериментов отбирались 6-8 образцов, а для графического представления использовались усредненные данные характеристик с коэффициентом вариации не более 10%.

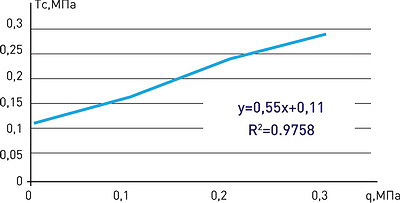
На рис. 17 представлены графики линейных зависимостей τс (q) для сухих образцов (W = 20%) первой (а) и второй (б) категорий плотности, данные которых свидетельствуют о том, что угловой коэффициент в уравнении Кулона tgφ = 0,45-0,55, что соответствует диапазону изменения угла внутреннего трения грунта φ = 0,25‑0,3°.

  б) 

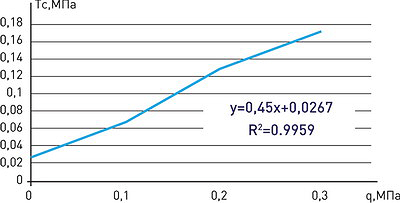
 а)

Рис. 17. Зависимость величины сопротивления сдвигу от вертикальной нагрузки

Свободные члены в полученных корреляционных уравнениях могут служить характеристикой сцепления грунта С_о. С ростом плотности среды величина С_о существенно возрастает.

Аналогичные опыты для образцов влажных почвогрунтов с ростом величины W до 35% свидетельствуют о том, что параметры линейной зависимости имеют тенденцию к снижению. В этом случае для группы образцов со средней плотностью ρ = 1,55 т/м³ обобщенная зависимость выглядит так:

τ_с = 0,35q + 0,0567 (R² = 0,9932).

Полученные данные с высокой степенью точности (коэффициент детерминации R² во всех экспериментах превышает 0,9) подтверждают правомерность принятого в математической модели закона Кулона для описания связи сдвиговых и нормальных нагрузок.

На втором этапе опытных работ осуществлялась проверка методического положения о том, что компоненты обобщенной сдвиговой (τ) и нормальной (q) нагрузки, отвечающие за достижение приведенного давления

С этой целью был поставлен эксперимент с использованием метрологически поверенного электронного динамометра сжатия ДОС-3-И разработки ООО «Петвес», в схему которого входят тензодатчик 101ВН и индикаторный терминал R320 для обработки результатов измерений с помощью специального программного обеспечения и ретрансляцией данных в приложениях Excel.

В ходе опытных работ фиксировались: эпюры вертикальных напряжений σ_в в зависимости от относительных деформаций ε_в образцов с получением зависимостей σ_в = f(ε_в); предельная нагрузка q, при которой образец разрушался, и соответствующие этому значению предельные величины относительной вертикальной ε_в и боковой ε_б деформаций. В силу однородности и изотропности материала используемых образцов определялась зависимость удельного сопротивления образцов сдвигу от боковой деформации τ = f(ε_б), которая сравнивалась с величиной вертикальной нагрузки q.

На рис. 18 для сухих образцов с ρ = 1,37-1,4 т/м³ и W = 20% представлен график зависимости σ_в = f(ε_в), которая хорошо описывается степенной зависимостью. Напряжения измерялись в МПа. Аналогичные графики получены для более плотных (ρ = 1,5-1,55 т/м³) и весьма плотных (ρ = 1,6-1,65 т/м³) образцов.

По достижении напряжений предельной разрушающей величины q = 0,071 МПа установлены значения относительных деформаций ε_в = 0,034 и ε_б = 0,022, после чего с помощью полученной зависимости 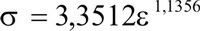была установлена величина τ = 0,044 МПа. Таким образом, отношение τ/q = 0,62 соответствует значению коэффициента Пуассона ν = 0,38.

На третьем этапе опытных работ оценивалось влияние цикличности вертикальных нагрузок на процесс уплотнения грунта.

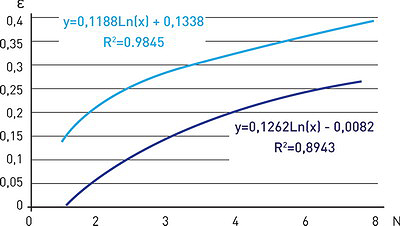
Рис. 19. Влияние цикличности нагрузок на развитие относительной деформации грунта: 1 – теоретическая зависимость величины ε от числа циклов проходов N; 2 – экспериментальная зависимость ε(N)

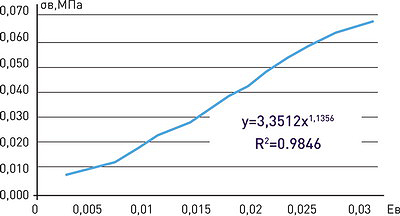
Рис. 18. График зависимости вертикальных напряжений от относительной деформации

В качестве постоянной (фиксированной) принималась нагрузка, равная 70-80% от предельной разрушающей нагрузки q.

На рис. 19 представлены: кривая 1 - теоретическая зависимость величины ε от числа циклов проходов N, которая соответствует зависимости (N) при нулевом угле поворота θ (см. рис. 6, кривая 1); кривая 2 - аналогичная экспериментальная зависимость ε(N) при плотности образцов ρ = 1,37 т/м³ и их влажности W = 20%.

Рис. 20. Вид эксперимента при повороте штампа в грунте

Количественное расхождение данных в силу отмеченных выше причин вместе с тем свидетельствует об удовлетворительном качественном совпадении теоретических и опытных результатов в процессе изучения на образцах закономерностей уплотнения грунта под воздействием циклических нагрузок.

Полученные результаты на образцах грунтов позволили спланировать эксперимент по изучению влияния угла поворота штампа θ на развитие касательных напряжений по мере удаления от направления волока (рис. 20).

С этой целью площадь индикаторной части тензодатчика была сокращена до s₁ = 2,89 см², а вес штампа увеличен до Q₁ = 200 Н. Такие параметры нагружения грунта адекватны развитию начальных напряжений под штампом, равных 0,692 МПа, что соответствует принятым в теоретической модели начальным нагрузкам при Q = 190 кН и площади штампа, равной s = 0,24 м² (для шести рабочих грунтозацепов), т. е. начальные напряжения составляют 0,79 МПа и отличаются от опытных значений не более чем на 10%.

Таблица 1. Экспериментальные данные при повороте штампа



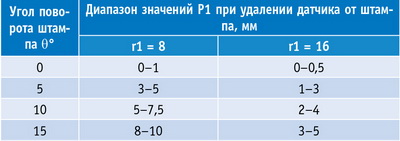
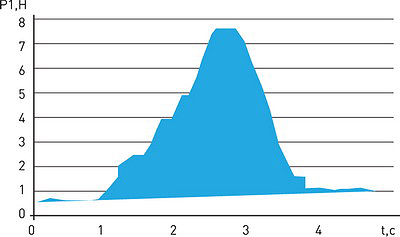
Рис. 21. Эпюра изменения силы воздействия поворота штампа на почвогрунт во времени

Величина удаления (r₁) от направления волока при опытных работах соотносилась с теоретической величиной r, исходя из подобия: отношение линейных размеров равно корню квадратному из отношения рабочих поверхностей. Оценивались два положения тензодатчика: в непосредственной близости к штампу (r = 0,25 м, т. е. r₁ = 7-10 мм) и в некотором удалении от него (r = 0,45 м, т. е. r₁ = 14-17 мм).

В табл. 1 приведены усредненные по 5-6 измерениям (с разбросом не более 15%) значения силы Р₁ (Н), действующей на рабочую поверхность датчика с площадью s₁ для двух указанных положений тензодатчика при его удалении от поверхности штампа.

На рис. 21 представлена после обработки в Excel 2007 типичная эпюра изменения величины Р1 во времени при нахождении тензодатчика в непосредственной близости датчика от штампа при повороте последнего на угол θ = 15°.

Полученные опытные данные напряжений были сопоставлены с расчетными значениями касательных напряжений τ_rθ (рис. 2) при соответствующих расчетным значениям величинах удаления уплотняемой зоны боковой полосы почвогрунта от трассы волока: первое положение r = 0,25 м; второе положение r = 0,45 м.

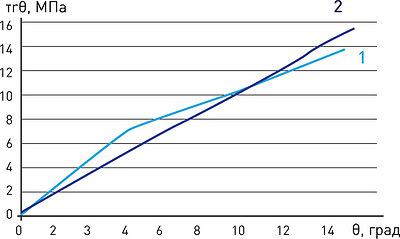
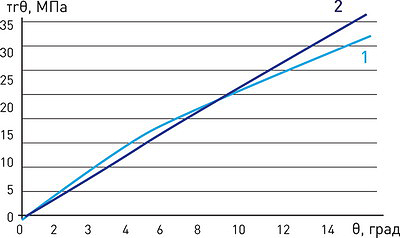
Результаты сравнительного анализа представлены на рис. 22 для двух положений удаления уплотняемой зоны боковой полосы почвогрунта от трассы волока - а и б соответственно, линии 1 - расчетные результаты, линии 2 - опытные.

2)

1)

Рис. 22. Сопоставление опытных и расчетных данных уплотнения зоны боковой полосы почвогрунта от трассы волока:
1 – теоретические данные; 2 – экспериментальные данные

Как следует из анализа данных, представленных на рис. 22, расхождение опытных и расчетных данных при первом положении ТС не превышает 10%, а при втором - 8%.

Таким образом, выполненные лабораторные исследования подтверждают основные методические положения при реализации математической модели циклического уплотнения грунта при возможном повороте трелевочной системы и формировании дополнительных касательных напряжений, усиливающих эффект уплотнения грунта в зоне, непосредственно прилегающей к трассе волока.

Полученные результаты дают основание использовать результаты математического моделирования при прогнозах развития процессов деформации грунта в боковых полосах волока с учетом возможных поворотов трелевочной системы.

Дмитрий ЛЕПИЛИН, канд. техн. наук, доц. каф. ТЛЗП СПбГЛТУ
Игорь ГРИГОРЬЕВ, д-р техн. наук, проф., зав. каф. ТЛЗП СПбГЛТУ