Энергоэффективность пеллетных прессов

Конструктивные факторы и силовой анализ

Сочетание конструктивных особенностей пеллетных прессов, главным образом, размеров и скорости вращения матрицы и количества роликов, делает каждую модель уникальной по характеру рабочего процесса. Прямым следствием является бóльшая или меньшая энергетическая эффективность либо производственный потенциал прессов при сопоставимой мощности двигателя.

При сравнении пеллетных прессов было установлено, что рабочая температура сильно варьирует (в пределе от 85 до 145 °С на сосне) в зависимости от модели при прочих равных условиях, а тепловой расчет, совмещенный с экспериментальными данными, показал разницу в итоговом КПД «на роликах» более полутора раз. Это означает, что одинаковая начальная кинетическая энергия от двигателя (одной мощности) используется с разной эффективностью. При этом КПД приводов разных типов дают относительную разницу до 8%, охлаждение роликов – до 6%, а тепловые потери без их учета достигают 43%.

Такой результат свидетельствует, что основной причиной потерь является не конструкция привода, а их возникновение непосредственно в материале и на границах «материал – инструмент».

Необходимо определить влияние конструктивных факторов на действующие силы процесса и совершаемую ими работу.

Факторы процесса пеллетирования

Известные конструктивные параметры:

• линейная скорость матрицы V_м, равная произведению частоты вращения и рабочей окружности матрицы n C_м;
• ширина рабочего фронта L_рф, равная произведению количества роликов на их ширину n_р В_р.

Для сравнительного анализа примем одинаковую заданную производительность прессов. Из этого следует, что количество (масса m и пропорциональный ей объем О) обрабатываемого материала в единицу времени t будут одинаковыми при разных факторах, как и количество получаемых пеллет.

m/t ~ О/t ~ SV (м³/с),

где m/t и О/t – массовая и объемная скорости материала соответственно,

S – площадь сечения материала под роликом в фазах сжатия и течения,

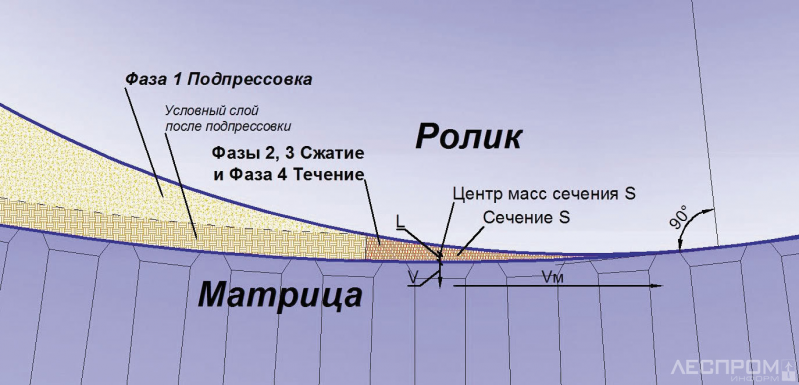
V – скорость движения материала (рис. 1).

При этом площадь сечения материала под роликом S обратно пропорциональна ширине рабочего фронта L_рф: S ~ 1/L_рф.

Среднее перемещение материала L должно учитывать элементарные расстояния ∆L для каждой частицы или элементарного объема пластичного компонента материала, движущихся по собственной траектории, в количестве n.

Тогда сумма Σ∆L_1...n будет коррелировать с площадью сечения материала под роликом S, а Σ∆L_1...n /n равна L – расстоянию от центра сечения материала (центра масс) до поверхности матрицы: L ~ S ~ 1/L_рф.

Скорость движения материала V прямо пропорциональна среднему расстоянию его перемещения L и обратно пропорциональна времени перемещения t.

Время перемещения материала t зависит от скорости матрицы V_м: чем она выше, тем t меньше и материал перемещается по направлению к поверхности матрицы быстрее.

V ~ L/t ~ (1/L_рф)/(1/V_м) ~ V_м/L_рф.

Рабочий фронт L_рф движется по поверхности матрицы с линейной скоростью V_м, оба этих параметра определяют характер процесса.

Механизм процесса пеллетирования и характер действующих сил

В распространенном представлении процесс состоит из трех фаз:

• сжатия опилок;
• течения материала по поверхности матрицы, затекания его в пресс-каналы;
• продвижения пеллет в пресс-каналах (фаза трения).

По существу фазы сжатия и течения совмещаются в той или иной степени, а разделение процесса на фазы нужно для описания его механизмов.

Имеет смысл разделить еще и первую фазу сжатия:

• сжатие материала до плотности древесины или подпрессовка – здесь будут работать только силы трения между частицами материала;
• сжатие материала свыше плотности древесины – требуется преодоление упругих свойств материала;
• сжатие материала выше предела прочности, при котором происходит разрушение внут­ренней структуры и уплотнение за счет межклеточного пространства – пластическая деформация (рис. 2).

Итоговый 5-фазный процесс (см. рис. 1) и действующие силы:

Фаза 1. Подпрессовка (выборка пустот между частицами материала) – силы трения.

Фаза 2. Сжатие материала выше плотности древесины до предела прочности – силы упругости.

Фаза 3. Сжатие материала выше предела прочности – силы пластической деформации.

Фаза 4. Течение материала, затекание его в пресс-каналы – силы вязкого трения и гидродинамического сопротивления.

Фаза 5. Продвижение пеллет в пресс-каналах – силы трения.

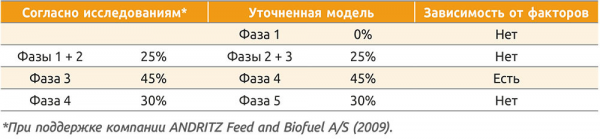
Энергозатраты фаз 1 и 5 не зависят от исследуемых факторов, а только от общего количества материала и пеллет, одинакового по условию сравнения. Кроме того, очевидно, что подпрессовка (фаза 1) требует незначительных затрат энергии в общем объеме работы. Исключаем эти фазы из расчета.

Силы и работа упругой и пластической деформаций (фазы 2 и 3) не зависят от исследуемых факторов – только от массы материала.

И лигнин, и целлюлоза – это полимеры аморфно-кристаллического строения, состоящие из разнотемпературных блоков с температурой течения 30–40 °С и ниже. И это без учета влияния давления, которое критично ее снижает. Поэтому невозможно полностью выделить фазы 2 и 3 из фазы 4, они протекают совместно.

Сила вязкого (внутреннего) трения – сила трения слоев условно жидкого (пластичного) компонента материала при движении относительно частиц материала, поверхностей матрицы и роликов. В фазе 4 появляется зависимость выполняемой работы от исследуемых факторов, в частности скорости перемещения материала V.

Фаза 4 (течения) оказывает решающее влияние на наблюдаемую разницу в энергобалансе.

Сила и работа фазы течения

Сила течения

Базовым законом вязкого трения является закон Ньютона: если параллельные плоские тела, каждое площадью S, находящиеся на малом расстоянии h, движутся в той же плоскости со скоростью Vтеч относительно друг друга, а пространство между ними заполнено жидкостью или газом, то на каждое тело действует сила, в простейшем случае пропорциональная относительной скорости V и площади S и обратно пропорциональная расстоянию между телами h:

F_теч = V_теч S/h.

Этот закон видоизменяется в зависимости от скорости движения и в общем случае принимает вид

F_теч = k_теч V_теч^1...3.

Значение коэффициента трения k_теч зависит от формы, размера и состояния поверхности тела и вязких свойств среды, а показатель степени скорости зависит от скорости и характеризует наличие завихрений. Например, считается, что квадрат скорости следует применять при движении (в воздухе) быстрее 70 км/ч (20 м/с), а третью степень – при скорости выше скорости звука. В подавляющем большинстве гидравлических законов фигурирует V_теч².

Как правильно определить физику течения при пелле­ти- ровании?

Основным механизмом является возникновение пластичного компонента на границах сдавливаемых частиц материала. Благодаря ему материал в массе становится подвижным и склеивается. Более глубокое расплавление может происходить в отдельных зонах с высоким давлением. Но и в этом случае это будет только тонкая пленка расплава толщиной не больше зазора между матрицей (вписанным цилиндром) и роликом (описанным цилиндром). Очевидно, что свободное течение материала отсутствует, его характер напоминает движение по капиллярам под давлением, что исключает завихрения.

Скорость течения очень мала и составляет всего n/100 м/с. Таким образом, можно утверждать, что F_теч ~ V_теч.

Работа течения

Обобщенно любую работу А можно свести к сумме произведений элементарных ∆F_n и ∆L_n для каждой частицы или элементарного объема пластичного компонента, перемещающихся по своей траектории. Или работа равна произведению суммы сил Σ∆F_1...n = F и среднего перемещения частиц L:

А = FL.

Невозможно разделить площадь сечения и перемещения материала в фазах 2–4 (см. рис. 1), однако, понятно, что они пропорциональны, а также пропорциональны S и L, отсюда

S_теч ~ S ~ 1/L_рф,

Lт_еч ~ L ~ S ~ 1/L_рф,

где S_теч и L_теч – площадь сечения и перемещение материала в фазе течения соответственно.

То же справедливо и для скорости течения:

V_теч ~ V ~ V_м/L_рф.

Итак, работа сил фазы течения пропорциональна V_м/L_рф²:

А_теч ~ F_течL_теч ~ V_течL_теч ~ VL ~ (V_мLрф) (1/L_рф) ~ Vм/L_рф².

Анализ результатов

Из технических характеристик пеллетных прессов для древесины установлено изменение влияющих конструктивных факторов в широком диапазоне.

Скорость матрицы V_м – от 3,5 до 7,9 м/с, то есть до 2,3 раза.

Ширина рабочего фронта L_рф – от 21 до 37,5 см, до 1,8 раза.

Исходя из полученной зависимости Атеч ~ V_м/L_рф², А_теч могла бы изменяться до 7,5 раза, хотя на практике до 2,5 раза.

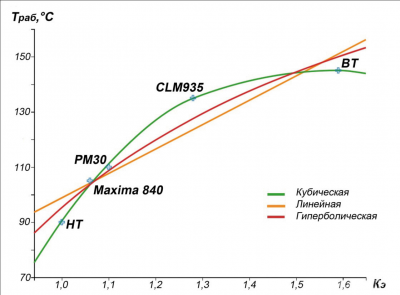
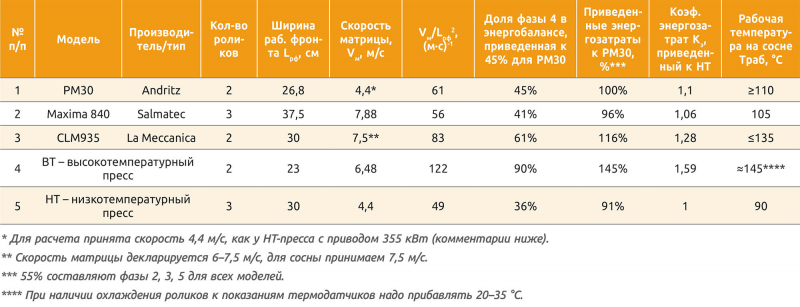
Для некоторых моделей прессов расчитаны относительные коэффициенты энергозатрат Кэ (табл. 1), а также определены несколько вариантов функциональной зависимости рабочей температуры Т_раб от К_э (рис. 3).

На графиках (см. рис. 3) приведены результаты в виде аппроксимации по трем функциям зависимости рабочей температуры Т_раб от К_э:

• кубической (r = 1; R2 = 1) y = 113,81x3 – 654,32x2 + 1204,71x – 573,80;
• линейной (r = 0,94; R2 = 0,88) y = 88,36x +10,43;
• гиперболической (r = 0,97; R2 = 0,94) y = 242,66 – 147,39/x.

Максимальное соответствие расчета эксплуатационным данным показала кубическая регрессия, а для практического анализа энергоэффективности проще применять гиперболическую или линейную функцию.

Рассмотрим две модели прессов с особыми сочетаниями факторов.

1. У Maxima 840 (рис. 4) самая высокая скорость матрицы, однако, за счет самого большого рабочего фронта температура прессования на сосне составляет всего 105 °С, что является вторым результатом в выборке. Конструктивно привод Maxima 840 представляет собой широкую группу прессов с многополюсным двигателем (n ˂ 1500 об-1) и одноступенчатой ременной передачей (аналогично CLM935).

2. Скорость матрицы РМ30 (рис. 5) декларируется от 3,5 м/с. Такая скорость использовалась для ранней версии пресса с мощностью привода 250 кВт. С такими параметрами РМ30 был лидером по энергоэффективности (Т_раб от 70 °С), однако его производительность составляла всего 3–3,5 т/ч, что несопоставимо с производительностью аналогов.

Более мощный привод (355 кВт) дает максимальное повышение производительности только вместе с одновременным повышением скорости матрицы. Но при неизменном L_рф энергоэффективность будет падать, а Т_раб – расти (см. табл. 1).

Достижение же низких скоростей матрицы стало возможным благодаря трехступенчатой редукции: двойной зубчатой и ременной передаче, ставшими уникальным решением.

Энергия рабочего фронта

Последний анализ касается такого технологически значимого параметра, как удельная плотность энергии на роликах.

Введем понятие удельной энергии рабочего фронта Е_рф, Дж/см², как отношения мощности привода Р, скорости матрицы V_м и ширины рабочего фронта L_рф (табл. 2):

Е_рф = Р/V_м/L_рф.

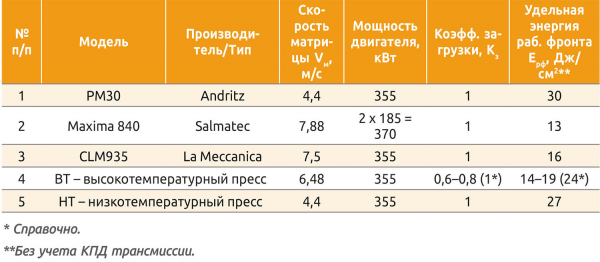
В физике в Дж/см² (Н/м) измеряют в числе прочих ударную вязкость и интерпретируют ее как скорость поглощения энергии материалом. В нашем случае это будет, наоборот, скорость подачи энергии. Этот показатель важен при пеллетировании сложных материалов, например древесины твердых лиственных пород. Удельная энергия рабочего фронта различается больше чем в два раза и выше у низкоскоростных прессов (см. табл. 2).

Поскольку этот параметр связан с мощностью привода, на него влияет и КПД трансмиссии (до 8%). Однако бóльшее влияние оказывает коэффициент загрузки К_з. Как уже отмечалось в предыдущей статье (ЛПИ. 2023. № 1), Кз искусственно ограничивают до 80% для ВТ-пресса, а рекомендуют использовать 60%.

Из вышесказанного следует, что наилучшая энергоэффективность достигается в трехроликовых прессах при современном уровне мощности привода примерно 350 кВт (табл. 3).

Почему нельзя повысить энергоэффективность двухроликовых прессов за счет увеличения ширины роликов? Если взять два пресса с одинаковым рабочим фронтом – НТ (три ролика по 100 мм) и CLM935 (два ролика по 150 мм) – и сравнить суммарный изгибающий момент (на все ролики), то у CLM935 он окажется на 15% больше.

Этот момент имеет два основных следствия: изгиб главной оси и давление на главный подшипник. А поскольку в двухроликовых прессах момент не уравновешивается матрицей, изгиб главной оси не ограничен, что приводит к более быстрому износу подшипников и даже излому оси.

Ширина роликов определяет механическую прочность конструкции, которая становится критическим фактором при увеличении мощности привода.

Выводы

1. Подтверждено различие прессов по энергоэффективности.

Силовой расчет показал разницу в выборке от 1 до 1,59, то есть больше 1,5 раза от энергозатрат НТ-пресса (Кэ = 1), что совпадает с результатами теплового расчета.

2. Определены основные влияющие конструктивные факторы – скорость матрицы и ширина рабочего фронта. Их оптимальное сочетание, соответствующее мощности привода, обеспечивает существенное повышение КПД пресса и его потенциальных возможностей. Наилучшее сочетание продемонстрировали трехроликовые прессы.

3. Наибольшая вариативность энергозатрат отмечена в фазе течения, которая составляет наибольшую долю в энергобалансе.

4. Вся работа так или иначе сводится к преодолению сил трения, которые почти полностью преобразуются в тепло. Рабочая температура является прямым показателем энерго- эффективности.

5. Получены теоретические зависимости, удобные для сравнительной оценки энергоэффективности на практике. 

Текст
Виктор Анисимов, Wood&Pellet Project