Взаимосвязь показателей древесины

Понимание взаимосвязи показателей древесины имеет большое практическое значение, особенно при использовании пиломатериалов и заготовок в строительстве, где прочностные и упругие свойства древесины важнее, чем внешний вид.

В европейской классификации пиломатериалов выделена специальная группа «Конструкционные пиломатериалы» с гарантированными прочностными показателями. При их сортировке измеряются модуль упругости или плотность древесины, на основании чего отбраковываются пиломатериалы, показатели которых ниже установленной нормы.

Основанием для разработки нормативов и настройки машин для прочностной сортировки пиломатериалов являются исследования взаимосвязи их показателей. Эти показатели можно разбить на две группы: одни определяются без разрушения материала, а другие требуют разрушения образцов при их испытании. К первой группе относят плотность, модуль упругости (статический или динамический), твердость древесины. Во второй группе пределы прочности древесины при различных воздействиях: сжатии, изгибе, растяжении, скалывании и в различных направлениях (вдоль или поперек волокон, в радиальном или тангенциальном направлении).

Таблица. Достоверность взаимосвязи (R²) показателей древесины
при влажности древесины 12%

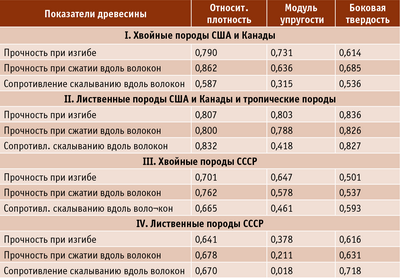
Рассмотрим взаимосвязь плотности, твердости и модуля упругости при изгибе с прочностными показателями чистой бездефектной древесины. В качестве исходной базы для расчетов возьмем результаты изучения физико-механических показателей образцов различных пород из различных районов произрастаний, выполненные соответствующими профильными исследовательскими институтами в Советском Союзе и США. Во внимание приняты три массива данных? для пород США и Канады, отечест¬венных пород и тропических пород древесины при влажности 12%. Различие сделано только между хвойными и лиственными породами. Как отдельная совокупность рассмотрены тропические породы.

Для характеристики связи двух величин использован показатель R2, называемый достоверностью аппроксимации, где R - коэффициент корреляции. В идеальном случае коэффициент корреляции равен 1, тогда на графике по осям координат X - Y все экспериментальные точки располагаются на прямой линии. Фактически коэффициент корреляции всегда меньше единицы, а на графике получается «рой» точек, группирующихся около прямой линии.

Помимо парных линейных уравнений (типа Y = aX + b), рассмотрены уравнения множественной регрессии, связывающие между собой три показателя: обычно какой-либо предел прочности и два показателя, определяемые без разрушения образцов, например плотность и модуль упругости. Линейное уравнение связи при этом имеет вид

Y = а + bХ₁ + сХ₂,

где Y - предел прочности;

Х₁ и Х₂ - показатели, замеряемые без разрушения образцов;

а, b, с - эмпирические коэффициенты, определяемые по экспериментальным данным.

Кроме линейных зависимостей, проверена также применимость нелинейных уравнений связи, а именно уравнений степенного вида Y = aХ^b.

Результаты расчетов достоверности взаимосвязи (достоверности аппроксимации) различных показателей чистой древесины обобщены в таблице.

В отличие от коэффициента корреляции, величина R² наглядно показывает, на сколько процентов один показатель зависит от другого. Например, для плотности и прочности при изгибе имеем
R² = 0,790. Это означает, что предел прочности при поперечном изгибе на 79% определяется плотностью древесины.

Изучение таблицы позволяет отметить следующие факты:

1. Наиболее тесную взаимосвязь с показателями прочности имеет плотность древесины. Графически это показано на рис. 1 для отечественных хвойных пород.

Уравнения связи имеют вид:

для изгиба σ_изг. = 0,325 ρ_баз.^0,879, ошибка 13,6%

для сжатия σ_сж. = 0,445 ρ_баз^0,737, ошибка 10,6%.

Аналогичные зависимости имеют место для всех остальных групп пород. В силу того, что в практике США и Канады используются для определения показателей чистой древесины образцы большего размера (сечением 51 х 51 мм), чем используемые в отечественной практике (сечение образцов 20 х 20 мм), объединять полученные результаты в одну статистическую совокупность не представляется возможным. Для того чтобы применить полученные уравнения связи для реальных пиломатериалов, требуется использовать поправочные коэффициенты, учитывающих среди прочего объем образцов, так называемый масштабный фактор.

 2. Твердость древесины также показывает хорошую взаимосвязь с пределами прочности (рис. 2).

Уравнения связи твердости с плотностью имеют следующий вид:

при изгибе σ_изг. = 15,08Т^0,497, ошибка 13,2%

при сжатии вдоль волокон σ_сж. = 8,89Т^0,489, ошибка 11,3%.

Оценка прочности по твердости возможна примерно с той же погрешностью, что и по плотности чистой древесины: ошибка уравнений связи составляет 10-15%. Показатель степени в уравнениях связи близок к 0,5, то есть прочность примерно пропорциональна величине  , где Т - замеренная твердость материала. При этом следует учесть, что в практике США и Канады твердость измеряется в килоньютонах (кН), а в нашей практике - в мегапаскалях (МПа), как отношение нагрузки к площади проекции отпечатка шарика.

3. Модуль упругости при изгибе уступает плотности и твердости древесины как для лиственных, так и хвойных пород во взаимосвязи с показателями прочности. Хорошая взаимосвязь наблюдается только для пределов прочности при изгибе и сжатии вдоль волокон.

Уравнения связи имеют вид:

при изгибе σ_изг. = 10,48Е^0,85, ошибка 11,11%

при сжатии вдоль волокон σ_сж. = 9,61Е^0,663, ошибка 10,85%.

4. При изучении взаимосвязи твердости с плотностью оказалось возможным рассматривать вместе все породы - лиственные и хвойные - и одновременно сравнить уравнения связи для древесных пород, произрастающих в разных полушариях нашей планеты (рис. 4).

Дело в том, что из множества показателей древесины только плотность и твердость определяются по совершенно одинаковым методикам в нашей стране и по стандартам АSТМ, хотя и в этом случае приходится пересчитывать наши показатели твердости из мегапаскалей в килоньютоны (10 МПа соответствуют 1 кН, так как площадь проекции отпечатка шарика составляет 100 мм²).

Как показывают рисунки, средние значения показателей близки друг к другу. Следовательно, можно говорить о практической адекватности уравнений связи, полученных из различных источников и характеризующих различные районы произрастания древесины. Поэтому в дальнейшем для решения вопросов нормирования показателей древесины мы используем данные по породам США и Канады, наряду с отечественными .

Из двух уравнений связи типа ρ_баз(Тв) мы рекомендуем первое уравнение как всеобщее уравнение связи боковой твердости древесины (кН) при влажности 12% с базисной плотностью (кг/м³)

 ρ_баз = 267Тв^0,438

Это уравнение имеет меньшую погрешность, чем полученное для отечественных пород, и потому кажется нам более соответствующим истине.

5. Совсем иначе обстоит дело с взаимосвязью модуля упругости и плотности древесины (рис. 5).

Видно, что плотность слабо коррелирует с модулем упругости древесины (R² = 0,435). Причина в том, что эти два показателя характеризуют разные стороны материала. Плотность есть мера пористости древесины, наличия древесинного вещества в единице объема. Модуль упругости же характеризует способность волокон деформироваться под действием нагрузки.

6. Наилучшие результаты при оценке вероятной прочности древесины может дать одновременный учет двух параметров древесины. Проведенные расчет дали следующее уравнение для оценки прочности при изгибе по модулю упругости Е и твердости Тв?

σ_изг = 6,035 + 4,428E + 8,782Tв

при достоверности апроксимации R² = 0,891.

Если модуль упругости определяет прочность при изгибе на 76%, а твердость - на 61%, то совместный учет двух показателей повышает достоверность оценки предела прочности до 89,1%. Соответственно этому снижается и ошибка уравнения связи: в первом случае она составляет 9,03%, во втором - 11,51% и в третьем - 6,08%.

7. Взаимосвязь разных пределов прочности также имеет серьезное практическое значение, так как позволяет, в частности, по результатам простых испытаний на сжатие вдоль волокон прогнозировать прочность древесины при изгибе и растяжении. Результаты наших расчетов показали, что для чистой древесины существует очень тесная связь пределов прочности при сжатии и изгибе (рис. 6). Это позволяет во многих случаях для характеристики какой-либо партии древесины ограничиться простыми испытаниями на сжатие вдоль волокон, на основании которых затем прогнозировать предел прочности при изгибе с погрешностью не более 7%. Сопротивление скалыванию связано с пределом прочности при сжатии гораздо меньше и не может быть прогнозировано через прочность при сжатии.

Еще более трудны испытания на растяжение вдоль волокон. Для отечественных пород связь пределов прочности при сжатии и растяжении выражается величиной R² = 0,4, что не позволяет говорить о надежном прогнозе. Однако при оценке по двум параметрам, то есть по формуле, учитывающей σ_сж и σ_изг, достоверность аппроксимации составляет 0,75. На рис. 7 показано соответствие фактических величин прочности при растяжении вдоль волокон теоретическим, рассчитанным по двум параметрам.

Следовательно, мы можем утверждать, что прочность при растяжении чистой древесины примерно на 75% определяется пределами прочности при сжатии и изгибе.

Все вышесказанное относится к малым чистым образцам древесины. При оценке прочности конкретных пиломатериалов необходимо учитывать ряд дополнительных факторов, но об этом мы расскажем в следующем номере журнала.

Владимир ВОЛЫНСКИЙ