Повышение эффективности групповой механической окорки лесоматериалов. Часть 6

Повышение эффективности групповой механической окорки лесоматериалов. Часть 1
Повышение эффективности групповой механической окорки лесоматериалов. Часть 2. Основные типы окорочных барабанов
Повышение эффективности групповой механической окорки лесоматериалов. Часть 3. Конструктивные элементы окорочных барабанов
Повышение эффективности групповой механической окорки лесоматериалов. Часть 4. Технологические характеристики процесса сухой окорки в барабанах
Повышение эффективности групповой механической окорки лесоматериалов. Часть 5. Размеры окариваемых лесоматериалов

В течение нескольких месяцев в нашем журнале читатели могли знакомиться с актуальными проблемами повышения эффективности групповой механической окорки лесоматериалов, о которых рассказывали сотрудники Санкт-Петербургского государственного лесотехнического университета. В заключение цикла мы предлагаем ознакомиться с некоторыми аспектами теоретических исследований процесса разрушения коры при групповой механической окорке лесоматериалов в окорочном барабане, в частности, с анализом методов расчета параметров и обоснованием математической модели разрушения коры при групповой окорке древесины.

Особенность реализации групповой окорки при использовании как барабанов, так и бункерных машин непрерывного или периодического действия заключается в реализации механизма взаимодействия бревен между собой и с элементами конструкций установок. Останавливаясь подробно на широко применяемой технологии барабанной окорки непрерывного действия, отметим основные физические механизмы при реализации этого процесса, а именно соударение бревен между собой и удары бревен о стенку барабана, в том числе при размещении на этой стенке специальных окорочных ножей.

В процессе барабанной окорки можно выделить в пределах пространства обработки пять разных зон, и наибольший интерес с позиций механики взаимодействия бревен в окорочном барабане представляют собой четвертая - зона обрушения, где бревна соударяются друг с другом, и пятая - зона удара, в которой бревна ударяются о стенку барабана или об размещенные на его внутренней поверхности рабочие органы.

Интенсивность очистки древесины от коры, качество окорки и потери древесины при этом процессе зависят от необходимого и достаточного числа ударов (N) определенной силы Р, которые испытывает бревно определенного диаметра (d) и длины (l) за период времени (t) нахождения в барабане, диаметр и длина которого составляют, соответственно, D и L.

Величины N и Р, в свою очередь, зависят от физико-механических, структурных и прочностных свойств сырья, их состояния (влажности W и температуры T), а также емкости барабана, степени его загрузки и угловой скорости вращения ω, определяющих в совокупности скорость (v) соударения поленьев как между собой, так и с конструктивными элементами барабана. В частности, при сухой окорке возникающие ударные нагрузки и силы трения при взаимодействии бревен являются недостаточными для качественной окорки сырья и необходимо использование специальных коронадрезающих ножей на внутренней поверхности барабана. Это обусловлено тем, что сухая кора деревьев обладает высоким сцеплением с прилегающим слоем древесины.

Стохастическая модель процесса соударений бревен в барабане предложена в работе российского ученого С. П. Бойкова, где качество окорки связано с продолжительностью обработки поленьев.

На основе биномиального распределения числа ударов, приходящихся на элементарную площадку Δs за период времени t, получено соотношение для определения математического ожидания (М) качества окорки:

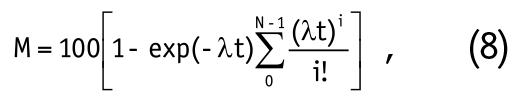
где λ - интенсивность ударов или среднее их количество, получаемых одним участком Δs в единицу времени. Величина N - основополагающий параметр соотношения (8) - зависит от силы удара Р и характеристик коры.

Основываясь на теоретических положениях этой модели, в исследовании, выполненном А. М. Газизовым и другими учеными, справедливо отмечается, что параметры N и λ не в полной мере отражают такой сложный процесс, как групповая окорка, и недостаточно учитывают закономерности ударных процессов в окорочном барабане в летний и зимний сезоны. В этой связи предложена математическая модель послойного перемешивания древесного сырья в окорочном барабане при положительных и отрицательных температурах. Влажность сырья, его физико-механические и прочностные свойства при этом учитываются не дифференцированно, а интегрально, путем введения специальных параметров.

Так, полученные в ходе выполненных исследований соотношения для определения скоростей движения коры и древесины содержат безразмерный параметр θ, названный А. М. Газизовым степенью сопротивления элемента коры удару, равный произведению циклической частоты колебаний на период продолжительности удара.

Число ударов N принимается равным отношению ударного импульса I_у, Н∙с, необходимого для появления пятна окорки площадью Δs, к величине ударного импульса I_о, Н∙с, возникающего при единичном ударе бревна в процессе его обрушения во вращающемся барабане.

Величину I_о определяют с учетом размеров бревна и барабана, а также угла наклона α поверхности обрушения.

Величина I_у в конечном счете устанавливается экспериментально в процессе нанесения по бревну акцентированных ударов с помощью специально созданных опытных установок. Суммированные значения ∑I_у и ∑Δs являются интегральными характеристиками необходимых силовых затрат для достижения поставленных технологических и качественных целей окорки в течение ее полного периода времени Т_о.

Суммарное количество ударов N_∑, которым подвергается вся совокупность элементарных участков Δs, определяется геометрическими параметрами баланса и барабана и может быть оценено с помощью соотношения:

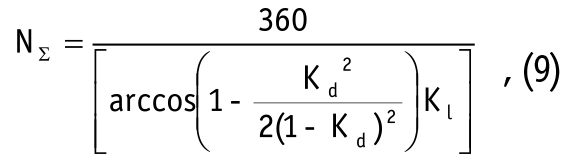
где коэффициенты K_d и K_l представляют собой отношения диаметра d/D и длины l/L соответственно.

На рис. 1а представлен график зависимости величины N_∑ от коэффициента K_d в диапазоне его изменения 0,035-0,077 и коэффициента K_l в диапазоне его изменения 0,13-0,52.

Как следует из рис. 1а, в процессе окорки материалов реализуются существенно разные условия по числу ударов N_∑, причем при уменьшении размеров балансов число ударов стремительно возрастает.

Объем коры ∑V_к в барабане зависит от объема V_б последнего, коэффициента его заполнения k_з, доли коры k_к в общей фитомассе ствола и - особо подчеркнем - от коэффициента K_n полнодревесности укладки бревен в барабане, который представлен на рис. 1б, и также зависит от безразмерных коэффициентов K_d и K_l.

Резюмируя результаты исследований А. М. Газизова, необходимо отметить, что они расширяют диапазон использования стохастической модели С. П. Бойкова, однако за рамками теоретического рассмотрения оказался сам процесс соударения бревен как между собой, так и с конструктивными элементами барабана.

Величину импульса I_у и процесс образования пятна окорки целесообразно оценить с позиций механики контактного разрушения такой сложной среды, как кора и древесина лесоматериалов.

Указанный подход нашел некоторое отражение в работе исследователя Ю. В. Никоновой, в которой на базе уравнений движения конечно-элементной модели изучены закономерности изменения сил контактного взаимодействия балансов при их соударении в корообдирочном барабане.

Ю. В. Никонова справедливо отмечает, что для определения таких сил необходимы данные о жесткости балансов, которые устанавливаются экспериментальным путем.

При этом балансы, взаимодействующие с поверхностью барабана, испытывают значительные по величине нагрузки за счет более высокой, чем у балансов, жесткости корпуса барабана. В свою очередь, само бревно испытывает неравнозначные по поверхностному распределению силы соударений, и в торцевых частях бревна наблюдается процесс их так называемого «размочаливания».

Основной научный результат работы Ю. В. Никоновой - прогноз объема балансов, при обработке которых сила соударений может оказаться недостаточной для качественной окорки древесины.

Однако и в этом случае рассмотренный процесс взаимодействия балансов не отражает особенности контактного разрушения разных участков массива коры и древесины как сложных структур, обладающих набором характерных физико-механических и прочностных свойств, влажностью и температурой.

Указанные параметры, как свидетельствуют результаты исследований А. М. Газизова, применительно к механической окорке с использованием как тупых короснимателей, так и фрезерных технологий, оказывают существенное влияние на все протекающие процессы отделения коры от древесины.

Следует полагать, что это влияние существенно и при реализации процессов ударного взаимодействия бревен как между собой, так и с поверхностью барабана, которая для повышения качества окорки в трудных условиях обработки может содержать специальные устройства и ножи.

На основании результатов выполненного анализа сформулируем основные положения для обоснования математической модели разрушения коры при групповой окорке лесоматериалов.

Бревно как совокупность цилиндров с диаметром и высотой d представим как совокупность равновеликих по объему шаров с диаметром D_ш= √1,5d. Количество шаров, приходящихся на одно бревно, равно целой части плюс единица отношения объема бревна V_бр к объему шара V_ш. Два крайних шара назовем торцевыми, остальные - внутренними. Все шары бревна принимаются как мягкие по отношению к жесткой поверхности барабана.

Выделим (рис. 2а) основные схемы взаимодействия мягких шаров с поверхностью барабана, которую, в свою очередь, будем рассматривать как жесткий шар D_ж с бесконечно большим диаметром D_ж=∞: схема I: «D_ш - D_ш» - взаимодействие двух мягких шаров; схема II: «D_ш - D_ж» - взаимодействие мягкого и жесткого шаров; схема III «D_ш - D_жи» - взаимодействие мягкого шара с жестким, на поверхности которого закреплен нож (твердый индентор).

Представленные схемы будем рассматривать в рамках постановки квазистатических задач ударного взаимодействия двух сферических контактирующих тел. Для обоснования математической модели и оценки ее адекватности на примере сравнения с опытными данными А. М. Газизова остановимся на схеме II (рис. 2б).

При воздействии ударной нагрузки силой Р основными геометрическими параметрами пятна контакта (его глубины и радиуса) являются величины контактного сближения h и радиуса контактной площадки a.

Эти параметры функционально связаны между собой, однако ударные процессы в механике контактного разрушения рассчитываются именно через величину сближения h, и с точки зрения качества окорки нас интересует очистка древесины на полную глубину коры. Поэтому в качестве основной геометрической характеристики контакта примем параметр h.

Будем считать, что по мере формирования пятна окорки контактная сила F растет и определяется в виде:

где коэффициент пропорциональности k зависит от упругопластических характеристик мягкого шара (модуля Юнга Е и коэффициента Пуассона μ) и его диаметра D_ш:

Дифференциальное уравнение движения среды на границе контакта при развитии пятна окорки вглубь массива коры выражается формулой:

где v - скорость движения бревна массой m в момент удара.

Наибольшее значение h=h_о достигается в момент времени, когда скорость сближения

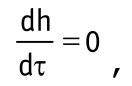
откуда величина максимального контактного сближения от единичного удара равна:

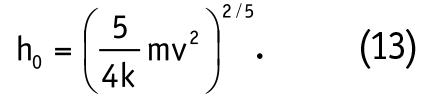
Общая продолжительность удара τ=τ_о при этом составит:

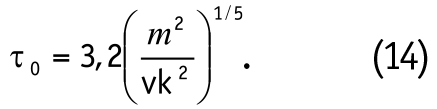
Интегрирование дифференциального уравнения (12) с учетом (13) при начальных условиях: в момент τ=0 сближение h=0 позволяет получить функцию изменения во времени контактного сближения h=h(τ):

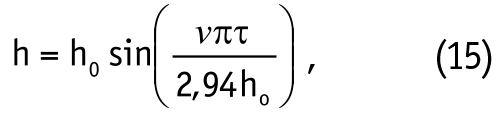
которую будем рассматривать на участке возрастания h от 0 до h_о.

Радиус контактной площадки а зависит от h и описывается соотношением:

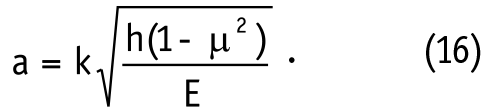
Силу удара Р вычислим следующим образом: вначале, используя закон сохранения энергии, определяем величину v=(2gH)^0,5, где H - высота обрушения бревен (максимальное значение H=D-d), а используя закон сохранения импульсов движения, - силу Р=mv/τ_о, причем, τ_о определяется формулой (14).

Расчеты с помощью соотношений (10)-(16) выполнялись таким образом, чтобы в максимальной степени учесть опытные данные, полученные исследователем А. С. Васильевым, в частности, применительно к условиям обработки летних балансов сосны влажностью W=40-60%, диаметром d=0,12 м, длиной l=2 м в окорочном барабане диаметром D=2,2 м и длиной L=4,3 м.

При таком диаметре бревна толщина коры сосны принимается h_к=0,02 м. Физико-механические свойства коры сосны принимались, исходя из данных, полученных А. М. Газизовым, с учетом влияния влажности W на изменение плотности коры ρ_к.

Так, для сухой коры при W=10% величина ρ_к=370 кг/м³, при W=40-60% плотность возрастает до ρ_к=687 кг/м³. Тогда масса бревна достигает m=15,55 кг.

Расчеты свидетельствуют, что в момент удара скорость соударения составила v=6,39 м/с, а продолжительность удара τ_о=9,62 мс. Контактная сила достигла величины Р=10,32 кН и обеспечила достижение максимальной глубины контактного сближения h_о=0,021 м, превышающей толщину коры h_к, т. е. в этом случае выполняется условие h_о≥h_к.

На рис. 3 представлены графики зависимости изменения по продолжительности времени удара h(τ) и а(τ) величин контактного сближения и радиуса контактной площадки. Контактное сближение в направлении z отстает от развития контактной площадки в радиальном направлении r (рис. 2б), и если возникающие в массиве коры в процессе ударного взаимодействия сдвиговые нагрузки qs достаточны для ее разрушения, то можно считать, что произойдет отделение этого участка на максимальную глубину h_о. Учитывая, что h≤a при любом τ, размеры разрушаемых площадок будем оценивать через величину h (оценка снизу).

Величину среднего вертикального давления q_z при ударном взаимодействии шаров (рис. 2б) определим, исходя из параметров h и D_ш:

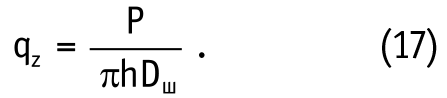
Величину радиального (горизонтального) давления определим с помощью механизма бокового распора:

после чего величину давления сдвига q_s на элемент коры определим как приведенное давление:

На рис. 4 представлена зависимость изменения во времени удара q_s(τ) величины приведенного давления в массиве коры летней сосны; расчеты выполнены при значениях μ=0,25 и Е=33,29 МПа, установленных с учетом корреляционных связей этих параметров с заданными физико-механическими характеристиками различных сплошных сред, включая лесоматериалы.

Сравнивая полученные значения q_s с величиной предела прочности не мерзлой коры сосны на скалывание σ_ск=0,33 МПа, можно сделать вывод о том, что с начального момента времени удара вплоть до достижения максимального сближения выполняется условие:

т. е. на полную глубину сближения h_o участок размером Δs =πh_o²=1385∙10^-6 м² будет полностью окорен. Величина ударного импульса при этом составила I_у=99,34 Н∙с.

Уместно отметить, что для мерзлых балансов сосны величина σ_ск≥1,1 МПа и возрастает до 1,8 МПа с понижением температуры до Т=-20^оС. Это означает, что в таких условиях установленные значения q_s недостаточны для реализации механизма сдвига в пределах элементарной площадки и не обеспечивают надлежащую окорку этого участка.

В этом случае необходимо либо увеличивать силовое воздействие, включая использование специальный ножей (см. схему III на рис. 2а), либо улучшать состояние балансов - обрабатывать их паром или горячей водой с целью снижения величины σ_ск до необходимого уровня. И в том, и в другом случаях для этого потребуются дополнительные затраты, а использование ножей обуславливает увеличение объемов потери древесины и «размочаливание» торцевых частей бревен.

Отметим, что влияние температуры на силы сцепления коры и процессы ее разрушения, а также особенности контактного разрушения при статическом внедрении индентора подробно рассмотрены в работах А. М. Газизова.

Возвращаясь к анализу условий обработки балансов летней сосны при выполнении условия (19), отметим, что для окорки элементарного участка достаточно одного удара о жесткую поверхность барабана, т. е. интегральные характеристики ∑I_у и ∑Δs совпадают с полученными одинарными значениями I_у и Δs.

Общий объем коры в обрабатываемых балансах для этих условий расчета составил ∑V_к=0,059 м³ при следующих значениях технологических коэффициентов: k_з=0,5, k_к=0,15 и K_n=0,36.

Максимально возможный объем разрушенной коры в пределах зоны контакта в результате единичного удара составляет V_к=πh_k³=127∙10^-6 м³, т. е. минимально необходимое число ударов по всем элементарным участкам балансов N_∑=465, что удовлетворительно согласуется с данными, приведенными на рис. 1а при значении коэффициентов K_d=0,055 и K_l=0,47.

Сравним полученные результаты с опытными данными А. С. Васильева, которые показывают, что для окорки аналогичных балансов также достаточно одного удара по элементарному участку коры при величине ударного импульса I_у=106 Н∙с с образованием пятна окорки площадью Δs=1486∙10^-6 м².

Таким образом, теоретические расчеты согласуются с опытными данными - относительная погрешность δ при оценке импульса составляет 6,7% при оценке размеров пятна δ=7,3%.

Выполним аналогичный расчет для условий окорки летних балансов осины с плотностью коры ρ_к=758 кг/м³ при W=40-60% и толщине h_к=0,05 м. Упруго-пластические характеристики: μ=0,25, Е=146,83 МПа. Масса бревна при этом составит m=17,15 кг, продолжительность удара τ_о=5,52 мс при максимальной силе Р=19,82 кН и ударном импульсе I_у=109,5 Н∙с.

Расчетные данные, аналогичные данным, приведенным на рис. 3 и 4, объединены и представлены на рис. 5 при том же временном масштабе (τ) и совмещенном масштабе: кривая 1 - h(τ) в см и кривая 2 - q_s(τ) в МПа.

Максимальное контактное сближение составило h_o=0,0112 м, а величина q_s достигла 1,26 МПа, но при этом превысила во всем диапазоне своего изменения значение прочностной характеристики немерзлой коры осины σ_ск=0,79 МПа. Отметим, что для мерзлой коры осины уже при Т≤ -10^оС величина σ_ск≥1,6 МПа.

Таким образом, для летних условий обработки бревна осины разрушение в пределах элементарной площадки Δs=456∙10^-6 м² на глубину h_o будет таким же, как и при окорке сосны. Вместе с тем, за один удар очистка массива коры произойдет только на глубину h_o=1,12 см, и для окорки баланса на полную глубину h_к=5 см потребуется не менее N=5 ударов.

На этом этапе обоснования математической модели мы не будем учитывать механизмы уплотнения коры в процессе циклического ударного взаимовоздействия с жесткой поверхностью барабана (индентора), т. е. принимаем, что на каждом новом цикле процесс удара воспроизводится в полном объеме.

Тогда получим: ∑I_у=NI_у=548 Н∙с и ∑Δs=NΔs=2284 10^-6 м².

Сравним полученные результаты с опытными данными А. С. Васильева при окорке бревен осины в аналогичных условиях. В данных, полученных А. С. Васильевым, установлены следующие показатели разрушения коры: N=7, ∑I_у=630 Н∙с (δ=14,96%) и ∑Δs=2350∙10^-6 м² (δ=2,89%).

При сравнении погрешностей расчетов для окорки кряжей сосны и осины выясняется, что при механическом воспроизводстве ударных процессов наблюдаются большие расхождения теоретических данных с опытными. Однако результаты расчетов следует признать удовлетворительными. Дальнейший учет в математической модели особенностей разрушения коры при циклических нагрузках, включая ее уплотнение и, как следствие, изменение упруго-пластических и прочностных свойств, приведет к росту необходимого числа ударов N и повышению точности оценок.

Анализируя результаты математического моделирования процессов контактного ударного взаимодействия мягкого шара (элемента баланса) с жестким шаром (поверхностью барабана), можно сделать вывод об адекватности принятых методических положений реальным условиям реализации процессов разрушения элементарного участка коры при групповой механической окорке.

Математическая модель для расчета технологических показателей групповой механической окорки мерзлых лесоматериалов

Приведенная выше математическая модель, описывающая процесс разрушения коры при групповой механической окорке лесоматериалов в окорочном барабане, позволяет детально рассмотреть предложенные схемы ударного взаимодействия I-III (рис. 2а) для разнообразных технологических условий групповой окорки лесоматериалов (в частности, при окорке мерзлых бревен), которая представляет собой сложный и трудоемкий технологический процесс.

Одним из основных параметров процесса групповой обработки лесоматериалов является период продолжительности окорки (τ_о). Переработка зимних балансов характеризуется увеличением показателя τ_о вследствие существенного (в несколько раз) увеличения предела прочности (σ_ск) коры на скалывание мерзлых балансов по сравнению с летними. На практике это приводит к ряду негативных последствий - увеличению потерь древесины при росте общих затрат, перекору, «размочаливанию» торцов бревен и др.

С целью интенсификации процессов отделения коры от древесины при низкой температуре (Т) на внутренней поверхности барабана устанавливают специальные ножи, которые, с одной стороны, обеспечивают достижение необходимого эффекта, но, с другой - способствуют дополнительному разрушению древесины, что снижает эффективность процесса окорки.

Интенсивность очистки древесины от коры, качество окорки и величина потерь древесины при барабанной окорке зависят от необходимого и достаточного числа ударов (N) определенной силы Р, которые испытывает бревно определенного диаметра (d) и определенной длины (l) за период времени (t) нахождения в барабане, диаметр и длина которого составляют D и L соответственно.

Величины N и Р зависят от физико-механических, структурных и прочностных свойств сырья, их состояния (влажности W и температуры T), а также от емкости барабана, степени его загрузки и угловой скорости вращения ω (числа n оборотов), определяющих в совокупности скорость (v) соударения поленьев как между собой, так и с конструктивными элементами барабана.

В результате исследований А. С. Васильева в рамках математической модели послойного перемешивания древесного сырья в окорочном барабане при положительных и отрицательных температурах для определения необходимого времени окорки τ_о получено соотношение, которое структурно можно представить как сложную функцию:

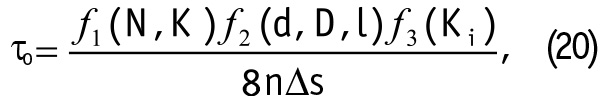
где

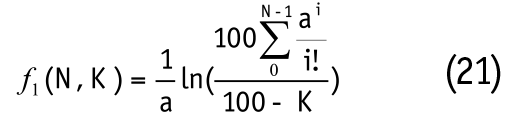
причем параметр - среднее количество ударов за время окорки τ_о;

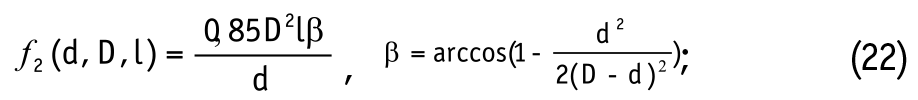
f₃(K₁), i=1, 2, 3, 4, - функция безразмерных коэффициентов: заполнения барабана (К₁), доли коры в общей фитомассе ствола дерева (К₂), полнодревесности (К₃), взаимосвязи толщины коры и диаметра бревна (К₄).

Анализ соотношений (20)-(22) показывает, что основными физико-механическими характеристиками ударного процесса при групповой окорке являются параметры N и Δs, которые в работе А. С. Васильева определены в ходе экспериментальных работ на специальной установке.

Установлено, что конечные параметры N и Δs зависят от соотношения между толщиной коры h_к и максимальной глубиной зоны контактного сближения h_о (рис. 2).

Из рассмотренных основных схем (рис. 2а) взаимодействия бревен (мягких шаров диаметром D_ш) с поверхностью барабана (жесткий шар с бесконечно большим диаметром D_ж=∞, в том числе - шар D_жи, оснащенный ножом - твердым интентором) на первом этапе исследований остановимся на схеме II с гладкой поверхностью окорочного барабана.

Математическая модель схемы II базируется на решении квазистатических задач ударного взаимодействия двух сферических контактирующих тел. При воздействии ударной нагрузки силой Р основными геометрическими параметрами пятна контакта (его глубины и радиуса) являются величины контактного сближения h и радиуса контактной площадки a.

В том случае (рис. 1б), если формируемое под действием силы Р в пределах контактного пятна размером Δs=πh_о² сдвиговое усилие q_s не меньше величины σ_ск по всей глубине h_о, то имеет место эффективный процесс отделения коры от древесины на полную глубину h_о.

Установим, каким образом температура Т влияет на величину предела прочности σ_ск и, как следствие, процесс образования глубины контактного сближения h_о. Эти исследования выполнялись на основании данных, полученных учеными М. Н. Симоновым и В. Г. Юговым в соответствии с положениями А. М. Газизова о влиянии фактора температуры Т на изменение свойств коры и развитие процесса ее разрушения.

На рис. 6 представлены полученные в ходе математического моделирования графики зависимости δs от σ_ск для коры сосны и осины.

Установленный экспоненциальный характер Δs(σ_ск) свидетельствует о том, при групповой окорке мерзлых балансов в процессе ударного взаимодействия бревен объемы разрушения резко снижаются, в результате чего количество необходимых ударов для очистки элементарного участка древесины от коры будет увеличиваться.

Этот вывод нашел подтверждение при оценке зависимости параметра N(T) для следующих условий окорки балансов сосны и осины: d=0,12 м, l=2м, D=2,2 м, L=4,3 м, n=10 об./мин., К₁=0,5, К₂=0,1 для сосны и К₂=0,18 для осины, К₃=0,35, К₄=0,0175 для сосны и К₄=0,0415 для осины. Заданное качество принято постоянным и равным К=90%.

На рис. 7 представлен график зависимости N от T для условий окорки балансов осины.

Анализ данных показывает, что при обработке мерзлых балансов древесины продолжительность процессов ударного взаимодействия бревен увеличивается кратно, что требует соответствующего увеличения технологического времени τ_о окорки материалов с учетом качества их обработки.

На рис. 8 представлены результаты оценки зависимости временного параметра окорки τ_о от температуры Т при окорке балансов сосны и осины с заданным качеством К=90%. Анализ данных, представленных на этом рисунке, свидетельствует о том, что при групповой окорке мерзлых балансов как сосны, так и осины параметр τ_о существенно возрастает по мере снижения Т и, в частности, при окорке осины при температуре ниже -10^оС превышает значение τ_о=60 мин. Повышение требований к качеству окорки также требует увеличения отрезка времени τ_о.

На рис. 9 для условий окорки балансов сосны представлены результаты исследований зависимости τ_о от качества окорки К и температуры балансов Т. Сравнительный анализ данных, представленных на рис. 9 и кривой 1 на рис. 8
 позволяет оценить степень увеличения параметра τ_о с изменением аргументов К и Т.

Данные, приведенные на рис. 8 и 9, позволяют оценить зависимость τ_о(К, Т) для условий окорки балансов осины. В этом случае значения τ_о в среднем возрастают в 1,4-1,6 раза по сравнению с аналогичными условиями окорки балансов сосны.

Таким образом, обработка мерзлых балансов при необходимости обеспечения высокого качества их окорки требует весьма значительных временных, а значит и материальных затрат. Выше отмечалось, что в этих условиях находят применение технологии окорки с использованием размещенных на внутренней поверхности барабана специальных ножей (схема III на рис. 2а).

В этой связи на втором этапе исследований рассмотрим процесс ударного взаимодействия массива коры толщиной h_к с ножом, размещенным на внутренней поверхности барабана. Будем считать, что нож, угол заточки (заострения) которого φ₁, взаимодействует с поверхностью коры под углом φ₂=π-φ₁/2.

Нож действует на поверхность коры с определенной силой удара Р и в зоне контакта площадью Δs формирует соответствующие силовые динамические нагрузки.

В работах А. М. Газизова и В. Я. Шапиро решена квазистатическая задача Буссинеска о внедрении твердого интентора (конуса, пирамиды, клина) в податливый упругий массив коры при фрезерных технологиях обработки лесоматериалов.

В плоской постановке в системе нормальной (вертикальной) z и радиальной (горизонтальной) r координат определялись значения соответствующих осевых давлений - q_z и q_r, после чего устанавливалась величина результирующего приведенного давление q_s, обуславливающего разрушение элементарного слоя коры на максимальную глубину контактного сближения h_о.

Установим с использованием методических положений А. М. Газизова закономерности влияния угла заточки ножа φ₁ на величину приведенного давления q_s.

Величину вертикального давления q_z определим в виде следующей формулы:

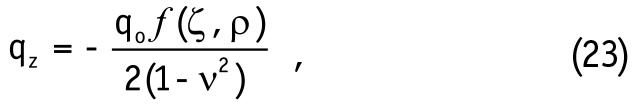
где f(ζ,ρ) - двумерная функция безразмерных координат - вертикальной и горизонтальной :

Величины b₀, b₁, α и β, входящие в формулу (24), определяются соотношениями:

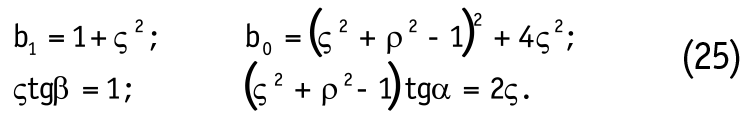
Величину начального контактного давления q_o определим как:

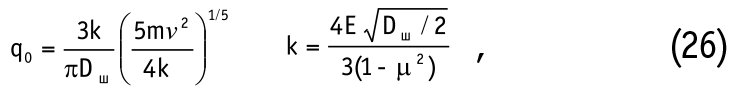
где: Е - модуль Юнга, μ - коэффициент Пуассона, m - масса бревна и v - скорость его ударного взаимодействия с контактом.

Величину горизонтального давления qr определим с помощью механизма бокового распора:

после чего величину давления сдвига q_s на элемент коры определим как приведенное давление:

Результаты выполненных исследований для сосны и осины представлены на рис. 10.

Кривая 1 на рис. 10 отражает зависимость безразмерного коэффициента k_q, характеризующего рост величины q_s по мере уменьшения угла φ₁ от 90^о (на поверхности барабана нет ножей) до 10^о (острый клин).

Кривая 2 отражает зависимость безразмерного коэффициента k_h, характеризующего рост величины h_o при аналогичном снижении угла φ₁.

Данные, приведенные на рис. 10, свидетельствуют о том, что использование ножей приводит к существенному (более чем в три раза) росту контактного давления и способствует почти двукратному увеличению максимальных размеров контактного сближения, что в свою очередь способствует росту размеров контактной площадки и увеличению ее площади Δs.

Выявленная тенденция роста Δs при использовании специальных ножей в соответствии с формулой (21) обусловливает уменьшение продолжительности окорки τ_о.

Исследования степени этого влияния и выполненные расчеты для условий окорки балансов осины без использования ножей и с их применением при угле заточки 30^о представлены на рис. 11.

Как следует из анализа данных, приведенных на рис. 11, применение ножей сокращает время обработки балансов в среднем в 1,5-2 раза, что повышает эффективность технологических процессов и снижает общие затраты на окорку. Вместе с тем, эта технология требует отдельного исследования в части изучения процесса динамического взаимодействия ножей с торцевыми частями бревен и установления таких ограничений на время окорки и такие параметры ножей, при которых будут минимизированы потери древесины и снижение качества окорки.

Таким образом, разработанная модель позволяет на стадии теоретических исследований оценивать один из основных параметров групповой окорки лесоматериалов - продолжительность их обработки с учетом конструктивных элементов барабана, параметров балансов, их свойств и температуры.

Игорь ГРИГОРЬЕВ, д-р техн. наук,
Борис ЛОКШТАНОВ, канд. техн. наук,
Ольга КУНИЦКАЯ, канд. техн. наук,
Антон ГУЛЬКО, аспирант,
 кафедра технологии лесозаготовительных производств СПбГЛТУ